컴퓨터를 만듭시다. 어때요~ 참 쉽죠? (12)
#12. 여러개 더하기. 반자동화
지난 번 만든 가산기는 분명 더하기를 하긴 하는데 단 두 개 숫자를 한 번 밖에 못한다. 8비트 가산기므로 0~255까지 숫자를 더할 수 있다. 물론 결과도 0~255 사이어야 캐리가 발생하지 않는다. 그래서 30 + 50을 원하면 80을 계산해서 출력해 준다. 하지만 30 + 50 + 70을 하고 싶다면 어떻게 해야 할까? 먼저 30과 50을 두 입력에 넣고 가산기의 CLK에 펄스를 한 번 준다. 그러면 출력으로 80이 나온다. 다시 80과 70을 입력하고 CLK에 펄스를 준다. 그러면 150이 출력될 것이다. 충분히 숫자 여러 개도 계산할 수 있다. 그러나 문제가 있다. 무엇일까? 기억을 사람이 대신해 줬다. 30과 50을 더한 80이라는 숫자를 사람이 기억하고 있다가 다시 입력해 준것이다. 지금까지 그렇게 열심히 컴퓨터의 기억 장치에 대한 이야기를 해 놓고서는 그것을 써먹지도 않았다. 오늘은 기억하는 가산기를 만들어 볼 것이다.
8비트 가산기에는 두 8비트 입력과 한 개의 8비트 출력이 있다. 내가 원하는 것은 이 가산기를 적절히 수정해서 8비트 한도 내에서는 계속해서 여러 개의 숫자를 더할 수 있도록 하는 것이다. 이것이 가능하려면 8비트 가산기의 출력으로 나온 8비트 값을 기억하고 있다가 다시 입력으로 넣어주는 동작이 필요하다. 가산기를 이야기하기 전에 기억에 대해 많은 이야기를 했었다. 이제 그것을 써먹을 차례다.
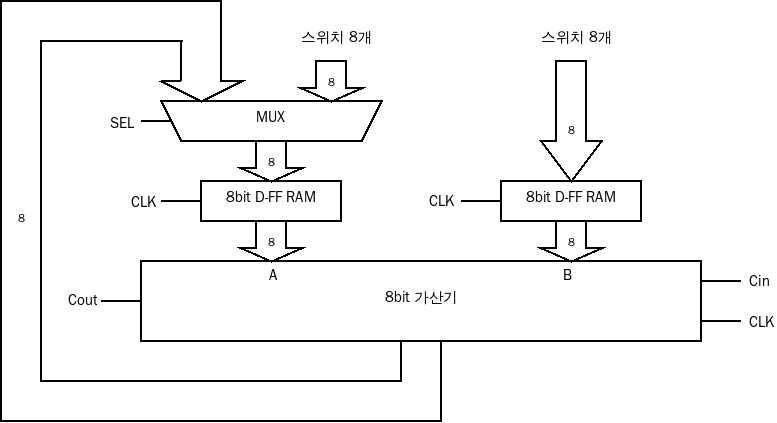
8비트 가산기의 두 입력에 D 플립플롭을 이용한 램을 붙이고 그 위에 스위치를 연결한 회로다. 화살표 안의 8은 화살표 한 개가 8비트 연결선 8개를 대신한다는 뜻이다. A 입력 쪽은 D 플립플롭 위에 MUX라는 것이 하나 더 붙어있다. 이것은 멀티플랙서(multiplexer)라는 것으로 입력으로 들어오는 신호를 선택해서 출력으로 보내주는 것이다. 위 회로에서는 16-to-8 multiplexer를 사용했는데 이것은 2-to-1 multiplexer를 8개 붙여놓은 것이다.

multiplexer는 간단히 mux라고 쓰고 먹스라고 읽는다. 나는 앞으로 그냥 먹스라고 쓰겠다. 2-to-1 먹스는 위 그림처럼 간단한 스위치로 만들어져 있다. 위 회로 역시 오래전에 이야기했었던 전자석과 스위치로 만들 수 있다. 추가로 스프링이 하나 더 필요하다. 오랜 추억을 되살려 한 번 그려 보겠다.

실제 반도체 소자의 구성은 위 그림과 다르겠지만 트랜지스터의 원리가 릴레이 스위치의 원리와 같은것처럼 먹스의 원리 역시 릴레이 스위치의 변형이다. SEL에 1을 입력하면 전자석이 동작하면서 스위치가 내려가 In_1의 입력이 OUT으로 나간다. 다시 SEL에 0을 입력하면 전자석이 꺼지면서 스위치가 스프링에 의해 올라가면서 In_0의 입력이 OUT으로 나간다.
위 그림의 먹스는 입력 두 개에 출력 한 개짜리 지만, 이걸 여러개 붙이면 입력 2n 개에 출력 n 개의 먹스를 만들 수 있다. 맨 위의 가산기 회로에도 16 입력에 8 출력 먹스가 쓰였다. 간단히 8 입력 4 출력 먹스의 내부를 보자.
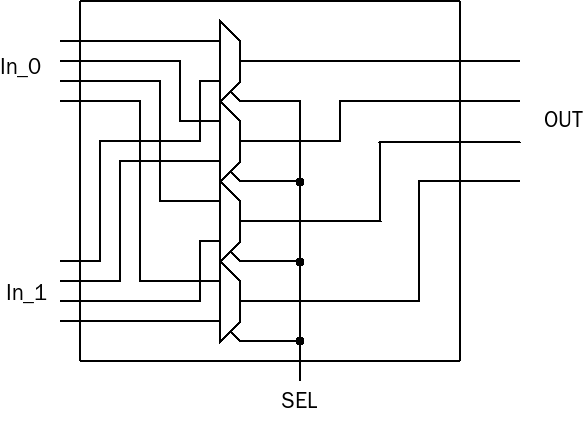
내가 사용한 16 입력 8 출력 먹스는 위 그림에서 2-to-1 먹스의 수를 4 개에서 8 개로 늘리고 회로 연결을 그대로 연장하면 된다. 8개를 다 그리면 그림이 밑으로 너무 길어져서 4개만 그렸다. 먹스라는 새로운 소자가 나와서 번외 설명이 길어졌다. 다시 가산기 회로를 보자.
먹스의 두 입력을 보면 한 개는 B 입력과 마찬가지로 스위치 8개의 8 비트 입력이다. 나머지 한 개는 빙 돌아 가산기의 출력 값이 입력으로 들어간다. 바로 이것이 있기에 오늘 이야기하는 가산기 회로는 직전 덧셈 결과를 저장 할 수 있는 것이다.
간단히 10 + 14 + 18 + 21 + 36 + 37 + 5를 해 보자. 참고로 이 숫자는 지난 주(357회) 로또 당첨 번호다. 기존 회로에서는 10과 14를 입력하고 출력으로 나온 24를 사람이 기억했다가 다시 24와 18을 입력하는 식으로 계산해야 했다. 오늘 바꾼 회로에서는 처음에 A에 10, B에 14를 입력한 후에는 결과 신경 쓸 것 없이 B에 18, 21, 36, 37, 5를 입력만 하면 마지막에 계산 결과가 남는다.
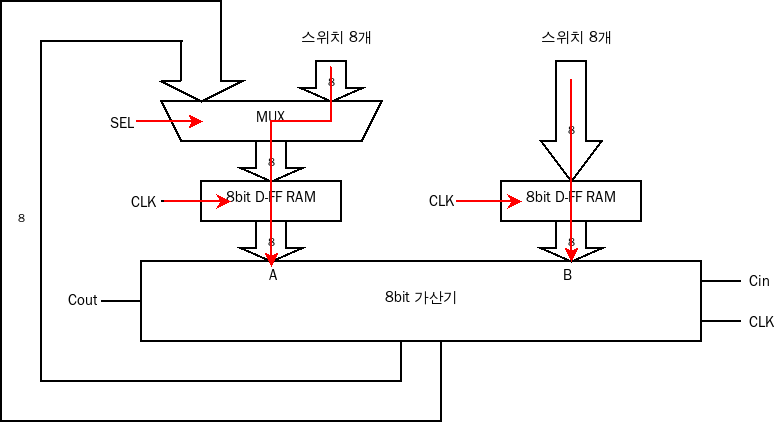
처음에는 A와 B에 초기 값을 입력하고 먹스의 SEL 핀을 1로 한다. 그러면 두 번째 입력이 출력으로 나간다. 그리고 A 쪽 D 플립플롭 램과 B 쪽 D 플립플롭 램의 CLK에 펄스 입력을 준다. 그러면 램에 저장되어 있던 값이 8비트 가산기로 들어간다. 이후 가산기의 CLK에 펄스 입력을 주면 계산을 완료해서 그 결과 값이 출력된다.
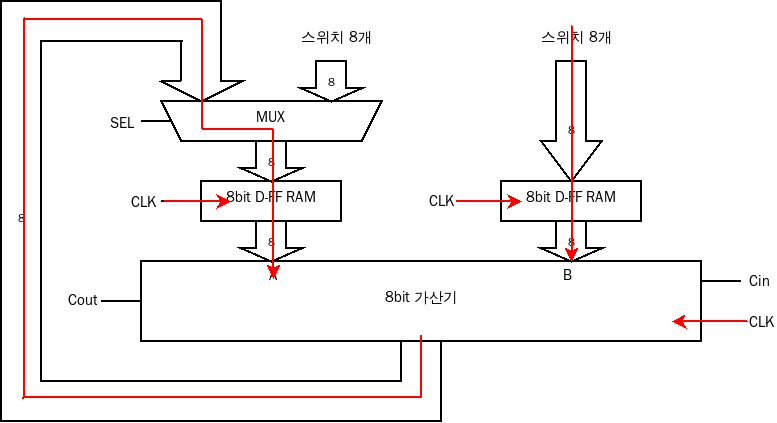
출력된 결과 값은 그대로 A 입력의 먹스로 간다. 이때부터 먹스의 SEL은 0을 유지한다. 그러면 첫 번째 입력이 출력으로 나가므로 가산기의 계산 결과가 A로 다시 들어가게 된다. B에는 덧셈을 하고 싶은 나머지 수를 계속 입력한다. 한 번 입력이 끝날 때 마다 D 플립플롭 램의 CLK에 펄스를 줘서 값을 가산기에 인가하고 A, B 입력이 끝나면 가산기의 CLK에 펄스를 줘서 계산을 한다. 이 과정을 계산하고자 하는 값을 다 입력 할 때 까지 반복한다. 마지막에 가산기에 남아 있는 값이 계산 결과가 된다.
가산기에 입력되는 값을 미리 작은 크기의 메모리에 저장해 놨다가 계산을 하게 되면 오늘 이야기처럼 어느 정도 자동화가 가능해 진다. 이와 같은 구조는 지금 이 순간 여러분이 쓰고 있는 컴퓨터나 핸드폰에 들어가 있는 CPU의 구조와 같다. D 플립플롭 램으로 만든 작은 메모리를 CPU에서는 레지스터라고 부른다.
우리는 오늘 레지스터에 값을 넣고 그 값을 가산기에 전달해서 덧셈을 하고 덧셈 결과를 다시 레지스터로 받는 회로를 만든것이다. 아직은 덧셈 밖에 할 줄 모른다 뿐이지 실제 CPU의 동작 원리를 아주 많이 따라왔다.
가산기에 레지스터를 붙이면서 인간이 신경써야 할 부분이 상당 부분 줄어들었다. 그리고 어느 정도 자동화가 된것 같기도 하다. 하지만 아직도 2% 부족하다. 앞으로 이 부족한 부분을 계속 채워나갈 것이다. 기대해 주시라.
| 첨부 | 파일 크기 |
|---|---|
| 12.52 KB | |
| 7.05 KB | |
| 5.09 KB | |
| 5.68 KB | |
| 12.82 KB | |
| 13.13 KB |


댓글
항상 그렇지만
열심히 보고 있습니다. 화이팅!
RAM에 값은 어디서?
가산기에서 초기 입력 10과 14을 램에 먼저 넣어놓고 시작하는건가요?
그리고 초기 값을 더한 결과 (24)가 A의 Mux로 가서 select 되고 다시 램으로 가는데 왜 24가 램의 인풋으로 들어가죠? 곧바로 가산기로 가야하는거 아닌가요?
제가 뭔가 잘못 이해하고 있다면 설명 부탁드립니다.
댓글 달기