컴퓨터를 만듭시다. 어때요~ 참 쉽죠? (7)
#7. 기억 두 번째 이야기.
오늘 이야기는 해야 할지 넘어갈지 약간 고민했다. 사실 자세히 다룰 필요없이 “이런게 있다~” 정도로 넘어가도 내가 하려는 이야기의 전체적인 흐름에는 전혀 영향을 주지 않는다. 하지만 고민 끝에 이야기를 쓰기로 결정했다. 자세히 다루면 한도 끝도 없고 적당히 하자니 이야기를 하는 나도 어려운 내용이고 이 이야기를 읽는 여러분도 이해하기 어려울 것이다. 미리 이런 말을 꺼내 놓고 시작하는 이유는 여러분이 부담을 가질 필요가 전혀 없다는 것을 강조하기 위해서다. 나는 열심히 그림 그려가면서 이야기하겠지만 여러분은 그냥 가볍게 읽고 넘어가 주기 바란다. 어찌 됐건 가벼운 이야기다.
지난 번에 이야기했던 RS 랫치는 NOR 게이트 두 개로 만들어진 피드백 회로를 일일이 그려서 표현 할 수도 있겠지만, 아래 그림 처럼 네모난 상자로 간단히 표현 할 수도 있다. 그리고 이렇게 간단하게 표현한 그림을 더 많이 사용한다.

앞으로 RS 랫치를 그릴 일이 있을 때는 위의 간단한 그림을 사용하도록 하겠다. 일일이 하나씩 게이트 그리는 것이 생각보다 손이 많이가고 귀찮다. 이해해 주기 바란다.
RS 랫치는 일시적으로 정보를 기억할 수 있는 회로다. 하지만 결정적인 문제가 있다. 출력으로 나가는 Q와 /Q의 값이 언제나 항상 보수 관계라는 법칙을 정해 놨기 때문에 두 입력 S와 R이 동시에 1이 되는 상황을 허용하지 않는다. 그래서 S에 1을 넣어서 값을 세팅하고 이 값을 기억하고 있다가 다시 지우기 위해 R에 1을 넣으려면 반드시 S에 0을 먼저 주어야 한다. 그렇지 않고 S에 1을 준 상태를 계속 유지하고 있다가 리셋을 하기 위해 단순히 R에 1을 준다면 순간적으로 R과 S가 동시에 1이 되어서 회로는 법칙을 위배하게 된다. 이 문제를 해결하고 싶다.

RS 랫치 앞에 AND 게이트 두 개를 붙이고 각 AND 게이트의 출력이 R과 S 입력으로 연결되었다. AND 게이트로 들어가는 입력은 두 개씩 네 개가 되는데 그중 두 입력은 CLK라는 이름으로 묶여 있고 남는 두 입력은 익숙한 이름인 S와 R로 붙여져 있다.
위 회로를 RS 플립플롭이라고 한다. 플립플롭과 랫치의 차이는 간단하게 플립플롭에는 클럭 입력(CLK)가 있고, 랫치에는 없다고 생각하면 된다. 더 깊게 들어가면 아주 많은 설명이 따라가야 겠지만 이정도만 알아놔도 상관없다.
AND 게이트는 두 입력 중 한 입력이 0일 경우 출력은 무조건 0이 되기 때문에 CLK가 0일 경우에 두 AND 게이트의 출력은 둘 다 0이 되면서 RS 랫치로 들어가는 입력도 모두 0이 된다. RS 랫치는 두 입력이 모두 0일 경우 값을 유지한다. 그러므로 CLK가 0인 동안은 RS 플립플롭의 R과 S 입력은 무엇이 와도 상관없다. RS 랫치에서 회로의 법칙이 깨질 가능성이 가장 높은 순간은 R과 S의 값이 바뀌는 순간이다. R과 S의 값을 바꾸기 전에 CLK를 0으로 놓고 바꾸면 회로가 한결 안정적으로 동작할 것이다. 위 회로의 진리표를 만들면 아래와 같다.
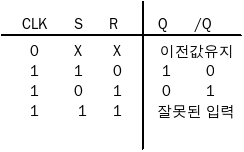
CLK 입력이 1일 때만 RS 랫치와 동일하게 동작한다. 그래서 CLK가 0인 동안 R과 S의 세팅을 변경할 충분한 시간적 여유가 있다. 하지만 아직도 R과 S가 동시에 1로 설정되었을 경우 법칙을 위배하는 문제는 해결 되지 않았다.
RS 플립플롭은 RS 랫치와 마찬가지로 아래 그림처럼 단순하게 네모 모양으로 표현할 수 있다.

RS 랫치와 다른 점은 R과 S 입력 사이에 CLK 입력이 하나 더 있다는 것 뿐이다. 역시 앞으로 RS 플립플롭은 위 그림을 사용할 것이다.
RS 플립플랍의 금지 조건을 해결하기 위해서는 어떻게 해야 할까? 해결 방법은 당연히 있다. 그것도 아주 쉬운 방법이다. 내가 해결 방법을 이야기해 주기 전에 여러분이 혼자 생각해 보기 바란다. 그리고 이제 내가 이야기하는 방법과 같은가 비교해 보라. 같은가? 같다면 당신은 천재다.

RS 플립플롭. 그리고 또 피드백 연결이 생겼다. 그리고 앞의 두 AND 게이트는 지금까지 봐 왔던 2-input-AND 게이트가 아니라 3-input-AND 게이트다. 입력이 두 개에서 세 개로 늘었을 뿐, 달라진것은 아무것도 없다. 입력 값 세 개를 AND 연산 하면 된다.
네모로 표현된 RS 랫치 안에도 피드백 회로가 숨겨져 있으므로 위 그림은 피드백 연결이 이중으로 되어 있는 회로다. 위와 같은 회로를 JK 플립플롭이라고 부른다. 실제 널리 알려져 있는 JK 플립플롭 회로는 RS 랫치까지 NAND 게이트를 이용해 만든 회로긴 하지만 위 그림도 동일하게 동작하니 너무 회로에 연연하지 말자. 중요한것은 동작에 대한 이해를 하는 것이다.
RS 랫치의 동작을 이해하고 있으면 JK 플립플롭의 동작을 이해하는 것도 어렵지 않다. 언제나 강조하지만 기본이 가장 중요하다. CLK가 0이면 두 AND 게이트의 출력은 항상 0이므로 RS 랫치에 전달되는 값도 항상 0이다. RS 랫치에서 두 입력이 모두 0이면 이전 값을 유지한다.
CLK가 1일 경우에는 J와 K의 입력에 따라 출력이 변한다. 일단 J가 1, K가 0일 경우를 보자. 피드백 연결이 있으므로 Q가 1일 때와 0일 때를 구분해서 봐야 한다. 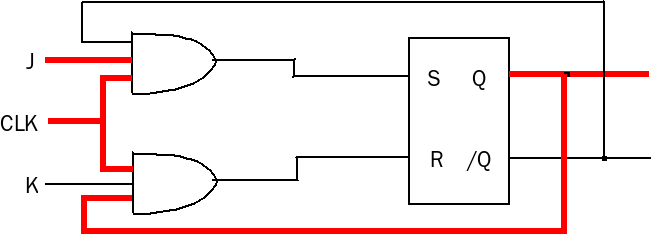
CLK는 1이므로 앞 쪽의 두 3-input-AND 게이트는 익숙한 2-input-AND 게이트로 생각해도 상관없다. J와 K의 입력은 1과 0이다. Q와 /Q도 1과 0이다. 피드백 연결로 인해 앞 쪽 두 AND의 출력은 0, 0이다. RS 랫치는 값을 유지한다. 그대로 Q=1, /Q=0이다. J와 K의 입력이 RS 랫치에 영향을 주진 않았고 Q와 /Q는 RS 랫치의 진리표와 일치한다.

J와 K는 여전히 1과 0이다. Q와 /Q는 전 그림과 반대인 0과 1이다. 피드백 연결로 인해 두 AND 게이트 중 J 쪽 AND 게이트의 출력은 1이 되고 K 쪽 AND 게이트의 출력은 0이 된다. 그러면 RS 랫치로 입력이 S=1, R=0이 되어 출력이 Q=1, /Q=0으로 바뀐다. 다시 피드백이 돌아 전 상황과 동일하게 되어 Q=1, /Q=0의 출력이 유지 된다.
최초 Q와 /Q의 상황이 다르지만 J, K의 입력에 따라 Q와 /Q의 출력값이 동일하게 동작한다. 역시 Q와 /Q는 RS 랫치의 진리표와 일치한다.
이제 J=0, K=1의 상태에서 Q가 1일 때, 0일 때를 보자.

J=0, K=1인 상태고 Q=1, /Q=0에서 피드백을 받아 앞의 두 AND 게이트의 출력은 위 그림과 같은 상태가 된다. K 쪽 AND 게이트의 출력이 1이 되므로 RS 랫치의 R 입력이 1이 되어 출력은 Q=0, /Q=1이 된다. 그러면 피드백이 다시 돌아 앞의 두 AND 게이트 출력은 둘 다 0이 되고 RS 랫치의 출력은 유지 되면서 Q=0, /Q=1을 유지하게 된다. RS 랫치의 진리표와 계속 일치하고 있다.

J=0, K=1의 상태에서 Q가 0일 때, 1일 때는 앞에서도 봤듯이 두 AND 게이트의 출력이 0이 되면서 값을 유지한다. J, K와 Q, /Q의 관계는 여전히 유지된다.
마지막으로 RS 랫치와 RS 플립플롭을 거치면서 계속 우리를 찝찝하게 만들었던 J=1, K=1일 경우에 대해 알아보자. 역시 직전 상태의 Q가 1일 때와 0일 때를 나눠서 생각해야 한다.
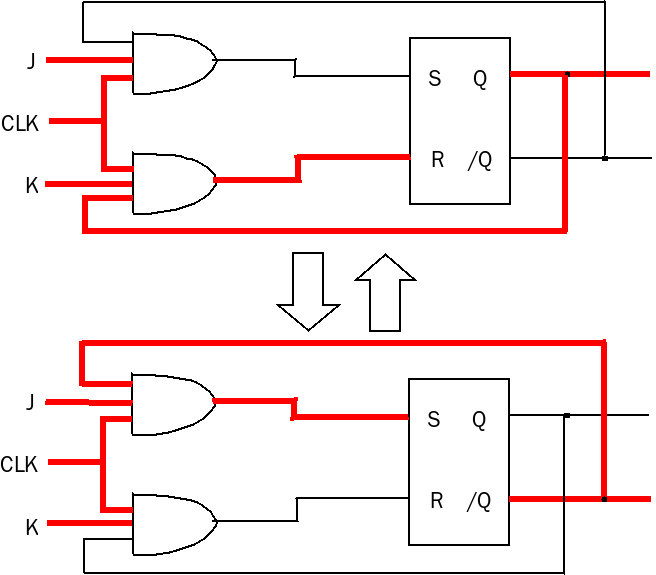
CLK와 J, K가 모두 1이므로 앞의 두 AND 게이트 출력을 결정하는 것은 피드백 신호다. 피드백 신호가 0이면 그대로 출력이 0이 되고 1이면 출력이 1이 된다.
RS 랫치의 출력을 서로 엇갈려서 피드백으로 넣었으므로 J 쪽 AND 게이트의 피드백 입력은 0이고, K 쪽 AND 게이트의 피드백 입력은 1이다. 그러므로 S=0, R=1이 되어 출력 결과는 Q=0, /Q=1이 된다. 이 값은 다시 피드백되면 또 값을 Q=1, /Q=0으로 바꾼다. CLK가 1일 동안 계속 Q는 0과 1의 출력을 반복한다.
J=1, K=1, Q=0, /Q=1일 때의 동작 역시 위 그림과 동일하다. 위 아래 순서만 바뀔 뿐이다.
역시 피드백 입력이 AND 게이트의 출력을 결정하므로 S=1, R=0을 입력으로 받게 되어 출력은 Q=1, /Q=0으로 바뀐다. 이 값은 다시 피드백 되어 값을 또 Q=0, /Q=1로 바꾼다. 마찬가지로 CLK가 1인 동안 계속 Q는 0과 1을 출력을 반복한다.
값이 반복되기는 하지만 Q는 /Q와 보수 관계여야 한다는 법칙을 철저히 준수하는 회로가 완성되었다. 놀랍지 않은가!
또한 값이 반복되는 것을 잘 보면 0과 1을 순서대로 반복하므로 이진 수 세계에서는 직전 Q의 출력과 반대되는 출력을 내 보내는 것으로 생각할 수 있다. 즉, J=1, K=1로 주면 직전 출력을 토글(togle)한다.
JK 플립플롭의 진리표를 그리면 아래와 같다.

J와 K 입력에 대한 출력 관계가 RS 플립플롭과 일치하면서 J=1, K=1일 때에 대한 금지 조건이 사라졌다. 뭔가 완성된 진리표를 보는 듯 하다.
그리고 지금까지 1로 고정시켜 생각했던 CLK에 대해 살짝 이야기 해보겠다. J=1, K=1일때 CLK를 계속 1로 고정 시키면 Q의 출력이 계속 바뀐다. 하지만 J=1, K=1일 때 CLK를 0으로 뒀다가 살짝 1로 올리고 다시 0으로 내린다면 Q의 출력은 직전 값의 반대 값으로 바뀌고 고정될 것이다.
마찬가지로 J와 K의 값이 다르게 설정되어 있더라도 CLK가 0에서 1로 올라가는 순간에 JK 플립플롭의 출력이 바뀐다. 만약 CLK에 전에 이야기 했던 오실레이터를 붙인다면 어떻게 될까?

오실레이터의 펄스 출력에 따라 동기화되어 규칙적으로 동작하는 JK 플립플롭이 될 것이다. 펄스 출력을 클록이라고도 한다. 그래서 CLK(CLocK)이라는 이름을 붙인 것이다. 클록이 빠르면 그만큼 빠르게 JK 플립플롭이 동작할 것이고 느리면 그만큼 느리게 동작할 것이다.

위 그림 같은 것을 타이밍 다이어그램이라고 부른다. 논리회로를 공부하다 보면 많이 보이는데 나는 여기서 한 번만 보여줄 생각이다. 단순해 보여도 한참을 보고 생각하고 있어야 해석이 되는 그림이기 때문이다. 내가 빨갛게 표시한 부분만 보면 된다. CLK가 0에서 1로 변하는 순간에 맞춰 Q와 /Q의 출력이 변하는 것을 알아보는 게 핵심이다. 그래서 JK 플립플롭의 진리표를 아래처럼 CLK 부분을 바꿔서 많이 표현한다.

오실레이터 펄스 출력이 변하는 순간은 두 종류가 있다. 전압이 0에서 1로 변하는 순간이고 1에서 0으로 변하는 순간이다.
0에서 1로 변하는 순간을 Rising Edge라고 부른다.

라이징 엣지라고 그냥 한글로 쓰기도 하고 상승 엣지, 상승 모서리, 올림 모서리 등으로 번역해서 쓰기도 한다. 나는 라이징 엣지라고 쓰겠다.
반대로 1에서 0으로 변하는 순간을 Falling Edge라고 부른다.

역시 폴링 엣지라고 그냥 한글로 쓰기도 하고 하강 엣지, 하강 모서리, 내림 모서리 등으로 번역해서 쓰기도 한다. 나는 폴링 엣지라고 쓰겠다.
클록 펄스가 1을 유지할 때나 0을 유지할 때가 아니라 라이징 엣지나 폴링 엣지에서 값이 변하는 소자를 엣지 트리거 타입 소자라고 부른다. 그래서 이 글에서 지금까지 이야기한 JK 플립플롭을 라이징 엣지 트리거 타입 JK 플립플롭이라고 부른다. 영어로 쓰면 Rising Edge Trigger Type JK Flip Flop이다. 와 길다. 게이트 선택과 구성에 따라서 폴링 엣지 타입으로 만들 수도 있다. 하지만 다루지 않겠다. 어차피 똑같다.
우리가 컴퓨터 CPU를 고를 때 1GHz니 3GHz니 하는 말을 많이 하면서 숫자가 높을 수록 빠른 CPU다라고 알고 있다. 이 1Ghz, 3GHz하는 말이 오실레이터의 클록 주파수라고 볼 수 있으며 숫자가 높을 수록 주파수가 빠르다는 뜻이고 CPU가 빠르게 동작한다는 뜻이다. CPU가 클록 주파수에 따라 빨라진다는 뜻은 결국 CPU를 계속 현미경으로 확대해서 들여다 보면 그 안은 플립플롭과 게이트로 이뤄져 있다는 뜻이다.
클록 입력까지 받는 플립플롭을 만들었다. 우리는 오늘도 조금씩 컴퓨터에 가까워 지고 있다.
| 첨부 | 파일 크기 |
|---|---|
| 2.55 KB | |
| 5.57 KB | |
| 5.41 KB | |
| 3.41 KB | |
| 5.76 KB | |
| 5.84 KB | |
| 12.45 KB | |
| 12.27 KB | |
| 5.83 KB | |
| 12.57 KB | |
| 4.4 KB | |
| 6.55 KB | |
| 45.61 KB | |
| 4.53 KB | |
| 2 KB | |
| 2.02 KB |


댓글
점점
점점 어려워지는군요..ㅠㅠ
쓰는 저도 정신이
쓰는 저도 정신이 혼미해 지더라는...
----------------------
얇은 사 하이얀 고깔은 고이 접어서 나빌레라
----------------------
얇은 사 하이얀 고깔은 고이 접어서 나빌레라
와우
잘 보고 갑니다ㅎㅎ 이해가 쏙쏙 !
togle -> toggle
togle -> toggle
SR flip flop에서
SR Latch 앞에 AND 게이트가 들어가는게 맞나요?
AND로 했을때 저런 진리표가 왜나오는지 이해가 안되네요..
NAND 게이트를 썼을때 위와같은 진리표가 나오게 되는거 아닌가요?
AND게이트가 맞습니다
간단히 말해서
CLK가 1일때는
R, S의 값이 흘러가고
CLK가 0일때는
R, S에 어떤값이 있어도
0으로 바뀌어 흘러가죠
클럭값을 1로 유지할 경우의 토글의 빈도는?
클럭값을 1로 유지할 경우 출력값이 계속 토글된다면 그 빈도는 어떻게 되는지요? 오실레이터를 통과할 경우와 어떤 차이가 있는지요? 초보자로서 궁금하여 질문드립니다.
댓글 달기