수학문제(analysis) sos ㅠㅠ
글쓴이: kkb110 / 작성시간: 토, 2010/11/27 - 10:55오후
자게니까 올려도 되나요? ^^; 부적절하다고 생각하시면 지워주세요~
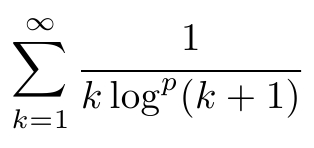
Analysis과목에서 나온 숙제중 하나 인데요, 그림으로 첨부했습니다. 그림의 식을 수렴하게 만드는 p를 구하고 증명하는 문제입니다.
p<=1 일때 발산하고 p>1일때 수렴하는데 증명을 못하겠네요.
다른문제들은 다 풀었는데 저것만 잘 모르겠어요;;;;;; 저 문제 나온 서브섹션에서 다룬 주제는 Integral Test, Comparison Test, Limit Comparison Test 세가지인데.. 이리저리 돌려봐도 생각보다 잘 적용이 안되네요 -_-;;;
File attachments:
| 첨부 | 파일 크기 |
|---|---|
 analysisproblem.jpeg | 13.32 KB |
Forums:
자답입니다. (Log[1+x]^(1-p))/(1-p)
자답입니다. (Log[1+x]^(1-p))/(1-p) 미분하면 거의 저 식이 나오는군요. integral test로 풀 수 있겠네요. -_-;;;
p가 log의 지수인가요? 아니면 log를
p가 log의 지수인가요? 아니면 log를 합성한건가요?
log의 오른쪽 위에 변수를 쓰는건 처음 보네요. 표기법좀 설명해주세요...
피할 수 있을때 즐겨라! http://melotopia.net/b
(Log(x+1))^p 과 같습니다~
(Log(x+1))^p 과 같습니다~
Integral test말고도
a_n 이 수렴하는거랑 a_{2^n} 이 수렴하는 거랑 동치임을 이용하면 풀 수 있습니다.
조금 더 자세히 설명해 주실 수 있으신가요? a의
조금 더 자세히 설명해 주실 수 있으신가요? a의 수렴성을 어떻게 s의 수렴성에 연결시키는지 감이 잘 안잡히네요.
p=0일때 발산은 증명된 거고, p<0일때 발산은
p=0일때 발산은 증명된 거고, p<0일때 발산은 그보다 크니까 당연히 발산하겠네요
p>0인 경우만 증명하면 되네요
피할 수 있을때 즐겨라! http://melotopia.net/b
아 잘못적었네요, p<=1 일때 발산하고 p>1 일때
아 잘못적었네요, p<=1 일때 발산하고 p>1 일때 수렴합니다. 지적감사합니다 수정할게요 ^^;
1이었군요 ㅡㅡㅋ
1이었군요 ㅡㅡㅋ
피할 수 있을때 즐겨라! http://melotopia.net/b