불가능에 한 표입니다.
두 실수 사이에 무한이 많은 실수가 있으니까요.
0 < a < 1인 a를 잡고
f(a) < 1이면 (a, f(a) + e1)을 왼쪽 아래로, (a + e2, f(a) + e3)를 오른쪽 위로 하는 사각형 하나 그리면 됩니다.
f(a) = 1이면 (a, f(a) - e1)을 왼쪽 위로, (a + e2, f(a) - e3)를 오른쪽 아래로 하는 사각형 하나 그리면 됩니다.
아, 불연속 함수를 고려 안 했나요? ㅠㅠ
더 생각해보죠.
begin{signature}
THIS IS SPARTA!!!!!n.
end{signature}
f(p) = a , f(p+Δp) = b 라면
필연적으로 |a-b| / Δp 라는 기울기를 가지게 되는데,
이리되면 x∈(p, p+Δp) 구간에서 사각형이 생길 수 있게 되죠...
다르게 얘기해서 기울기를 가지는 순간에 (그러니까 어떤 구간에서든 미분이 가능하다면)
이미 그 함수는 평면을 커버하고 있지 않은거죠.
덧)
만약에 기울기란게 없다, 모든 구간에서 미분 불가능하다...라고 했을 경우....
세 개의 연속된 수를 a,b,c로 표현했을 때,
x∈(a,c) 구간 내부에서
y∈(0, min(f(a),f(b),f(c)))
y∈(min(f(a),f(b),f(c)), median(f(a),f(b),f(c)))
y∈(median(f(a),f(b),f(c)), max(f(a),f(b),f(c)))
y∈(max(f(a),f(b),f(c)), 1)
중 한가지 구간에서 사각형을 만드는게 가능합니다.
실수에서 '연속된 수'라는 개념은 사용할 수 없을 것 같습니다.
"실수 a 오른쪽으로 연속된 수"를 정의해보자면 "a보다 크면서 다른 모든 a < 실수들 보다는 작은 수" 정도가 될텐데
연속된 숫자 b 있다고 가정하면, a < (a+b)/2 < b 가 되어 b는 정의상 연속된 수가 될 수 없습니다. Contradiction.
(함수가 C1 이라는 가정 하에) 기울기로 보자면.. f(p) = a , f(p+Δp) = b 사이에선 기울기 (b-a)/Δp인 점이 최소한 한곳 이상 있는것은 맞는데
빈공간이 있다는걸 보이기 위해선 조건이 좀 더 필요할 것 같네요. 여전히 0과 1 사이를 요동칠 수 있으니깐요. 그냥 연속성가지고 논하는게 간단해보입니다.
함수가 미분가능하면 연속(continuous)이고, 연속함수의 epsilon-delta 정의를 써서 모든점에서 사각형을 명시적으로 구축가능합니다.
[0,1]과 [0,1]X[0,1]이 cardinality가 같다는 점은 이 문제와는 별 관계는 없을 것 같습니다.
왜냐하면 둘의 cardinality가 같다는 것은 g: [0,1] -> [0,1]X[0,1]인 bijection g가 있다는 것인데요..
이문제에서는 애초에 f:[0,1] -> [0,1]을 제시하라고 했기 때문에 g(x) = (x, f(x))를 만족해야 합니다.
그런데 이러한 bijection은 존재하지 않습니다. 간단한 예로만 봐도 g(x1)=(0,0)이라고 하면 g(x2)=(0,1)이 되는 x2는 있을 수 없죠.
따라서 제 생각에는 어떤 f:[0,1] -> [0,1]도 [0,1]x[0,1]의 모든 점을 커버할 수는 없기 때문에
애초에 문제에서 주어진 "면적이 있는" 직사각형이라는 점을 이용해야 될 것 같습니다.
유리수 집합 Q={p_1,p_2,...}이라 하면
take q_1 from R-Q
Q_1={p_1+q_1, p_2+q_1, p_3+q_1,....}
take q_2 from R-(QUQ_1)
Q_2={p_1+q_2, p_2+q_2, p_3+q_2,....}
take q_3 from R-(QUQ_1UQ_2)
Q_3={p_1+q_3, p_2+q_3,.....}
:
:
0.we can construct Q_n for all n in N. (R uncountable)
1.Q_i, Q_j disjoint subsets of R for i!= j.
2.Q_i dense in R for all i.
f(x)=p_i if x in Q_i for some i, 0 otherwise.
then {(x,f(x))} dense in RxR.
위의 Jick님의 함수 잘 들여다 보세요. 예로 큰 소수 p에 대해서, {(k/p,(mp+k)/p^2)| p prime, 0<= m, k<=p-1} 점들을 생각해보시면 됩니다. 제가 했던 방법 쓰시려면 Q_i={q/(p_i^n)|p_i is i-th prime, n in N, q in Z, gcd(p_i,q)=1 } 집합들을 생각하시구요. 저는 여기까지만.
clarification
그래프에 그려진 함수는 y = x로 보입니다. 어느 쪽이죠?
그리고 원하는 함수는 F: R x R -> R x R 이 옳은가요?
...And all in war with Time for love of you,
As he takes from you, I engraft you new.
-Sonnet XV
전산계획설계사 지망 영문학과생
함수는 R->R, [0,1] -> [0,1]
함수는 R->R, 1차원.. 여기서는 [0,1] -> [0,1] 입니다.
단 사각형을 이야기는, 함수의 그래프, 2차원 평면 RxR 입니다.
+그림수정했습니다 지적 감사 ^^;
직사각형을 굳이 정의하자면, 다음이라고
직사각형을 굳이 정의하자면, 다음이라고 합시다.
[a,b]x[c,d] where
a,b,c,d∈[0,1]
a!=b
c!=d
a≠c ∧ b≠d 겠죠... 좀더 제약을
a≠c ∧ b≠d 겠죠...
좀더 제약을 건다면
a<c ∧ b<d 정도...?
아...
f(x)가 2차원 전부를 뒤덮으면 되겠군요
피할 수 있을때 즐겨라! http://melotopia.net/b
네, 2차원을 덮는 예제 f 를 하나 보여주시거나,
네, 2차원을 덮는 예제 f 를 하나 보여주시거나, f가 2차원을 다 덮을 수 없다는걸 증명하면 됩니다 :)
증명할 필요가 없이 함수의 정의가 뭔지를 제대로
증명할 필요가 없이 함수의 정의가 뭔지를 제대로 이해하면 되는겁니다.
함수는 관계중에 x값 하나에 대응하는 y값이 유일한 것들만을 말하는 것이니까,
[0,1]을 하나의 원소로 가지는 집합이라면 함수로 정의되지만, [0,1]이 (진)부분집합으로
가지는 공변역을 가지는 함수는 정의상 존재할 수 없다는거를 말해주면 증명이라고 받아들일라나요?
저도 그런 줄 알았는데 다가함수라는게
저도 그런 줄 알았는데 다가함수라는게 있더라구요.
http://en.wikipedia.org/wiki/Multivalued_function
근데 다가함수가 나와버리면 문제가 성립
근데 다가함수가 나와버리면 문제가 성립 안하지않나요...?
음냐.
popcorn function을 어떻게 대충 건드리면 됩니다.
...And all in war with Time for love of you,
As he takes from you, I engraft you new.
-Sonnet XV
전산계획설계사 지망 영문학과생
popcorn function이 이거 맞나요? 혹시
popcorn function이 이거 맞나요? 혹시 찾아보실 분들이 있을거 같아서 그림첨부합니다.


페아노 곡선을 응용하면 될 것 같은데요
페아노 곡선을 응용하면 될 것 같은데요
피할 수 있을때 즐겨라! http://melotopia.net/b
페아노곡선은 2차원 곡선 아닌가요? R->RxR
페아노곡선은 2차원 곡선 아닌가요? R->RxR
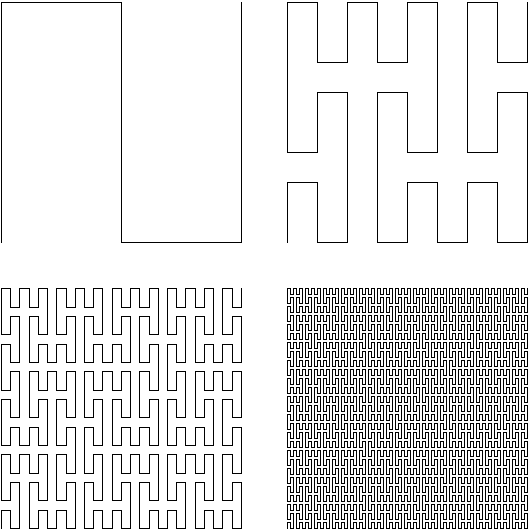
일단 F:[0,1] -> [-inf, +inf]로
일단
F:[0,1] -> [-inf, +inf]로 보내는 함수가 있습니다. F = log(x)
[-inf, +inf] -> 페아노 곡선 위의 한 점
정확히 어떤 형태가 될지는 모르겠지만, 페아노 곡선 위의 한 점을 0에 대응시키고, 그로부터 양쪽으로 무한대까지 대응시키면 됩니다.
수학적으로 엄밀히 증명하는건 일단 생략합니다. 바빠서요...-_-
피할 수 있을때 즐겨라! http://melotopia.net/b
2차원을 다 덮는게 함수인가요?
2차원을 다 덮는게 함수인가요?
그러면 2차원을 다 덮으면 함수가 아니라는걸
그러면 2차원을 다 덮으면 함수가 아니라는걸 증명하시면 됩니다~
근데 문제에서 필요한 '다 덮는다'라는게.. 항상 x에 대응되는 y가 여러개야 만이 가능한걸까요?
불가능에 한 표입니다.두 실수 사이에 무한이 많은
불가능에 한 표입니다.
두 실수 사이에 무한이 많은 실수가 있으니까요.
0 < a < 1인 a를 잡고
f(a) < 1이면 (a, f(a) + e1)을 왼쪽 아래로, (a + e2, f(a) + e3)를 오른쪽 위로 하는 사각형 하나 그리면 됩니다.
f(a) = 1이면 (a, f(a) - e1)을 왼쪽 위로, (a + e2, f(a) - e3)를 오른쪽 아래로 하는 사각형 하나 그리면 됩니다.
아, 불연속 함수를 고려 안 했나요? ㅠㅠ
더 생각해보죠.
begin{signature}
THIS IS SPARTA!!!!!n.
end{signature}
f_0(x) = 2x (0 <=x <= 1/2)
f_0(x) = 2x (0 <=x <= 1/2)
1 - 2x (1/2 <=x <= 1)
f_n(x) = f_{n-1}(2x) (0 <=x <= 1/2)
f_{n-1}(2x-1) (1/2 <=x <= 1)
n을 무한대로
begin{signature}
THIS IS SPARTA!!!!!n.
end{signature}
각 fn은 함수이지만 fn이 함수로 수렴하는지 증명이
각 fn은 함수이지만 fn이 함수로 수렴하는지 증명이 필요한 것 같습니다.
f(x) = lim(x->∞) sin^2
f(x) = lim(x->∞) sin^2 (n*x)
는 훼이크....
이 경우엔 함수값이 존재하질 않습니다 - ㅅ-)
그리고 아마도 존재하지 않을듯 싶습니다만...
f(p) = a , f(p+Δp) = b 라면
필연적으로 |a-b| / Δp 라는 기울기를 가지게 되는데,
이리되면 x∈(p, p+Δp) 구간에서 사각형이 생길 수 있게 되죠...
다르게 얘기해서 기울기를 가지는 순간에 (그러니까 어떤 구간에서든 미분이 가능하다면)
이미 그 함수는 평면을 커버하고 있지 않은거죠.
덧)
만약에 기울기란게 없다, 모든 구간에서 미분 불가능하다...라고 했을 경우....
세 개의 연속된 수를 a,b,c로 표현했을 때,
x∈(a,c) 구간 내부에서
y∈(0, min(f(a),f(b),f(c)))
y∈(min(f(a),f(b),f(c)), median(f(a),f(b),f(c)))
y∈(median(f(a),f(b),f(c)), max(f(a),f(b),f(c)))
y∈(max(f(a),f(b),f(c)), 1)
중 한가지 구간에서 사각형을 만드는게 가능합니다.
실수에서 '연속된 수'라는 개념은 사용할 수 없을 것
실수에서 '연속된 수'라는 개념은 사용할 수 없을 것 같습니다.
"실수 a 오른쪽으로 연속된 수"를 정의해보자면 "a보다 크면서 다른 모든 a < 실수들 보다는 작은 수" 정도가 될텐데
연속된 숫자 b 있다고 가정하면, a < (a+b)/2 < b 가 되어 b는 정의상 연속된 수가 될 수 없습니다. Contradiction.
(함수가 C1 이라는 가정 하에) 기울기로 보자면.. f(p) = a , f(p+Δp) = b 사이에선 기울기 (b-a)/Δp인 점이 최소한 한곳 이상 있는것은 맞는데
빈공간이 있다는걸 보이기 위해선 조건이 좀 더 필요할 것 같네요. 여전히 0과 1 사이를 요동칠 수 있으니깐요. 그냥 연속성가지고 논하는게 간단해보입니다.
함수가 미분가능하면 연속(continuous)이고, 연속함수의 epsilon-delta 정의를 써서 모든점에서 사각형을 명시적으로 구축가능합니다.
길게 말할 것없이 실수에 연속된 숫자란게 있을리
길게 말할 것없이 실수에 연속된 숫자란게 있을리 만무하죠 [먼산]
원래는 N을 R에 맵핑했다고 하고, 여기서 연속된 세 자연수에 매핑된 실수를 가리키는 거였는데
저거 쓸 당시에는 왠지 모르게 머리가 안돌아가서 일단은 저렇게 써버렸습니다 = ㅅ=)
그리고 확실히 기울기 가지고 불연속 함수에 대해 이야기하는건 좀 어불성설이지 싶습니다.
모든 구간에서 미분이 불가능한 함수도 존재하고 말이죠 - ㅅ-)
...
f(x) = (p mod q) / q, if x = p/(q^2), (p와 q는 서로 소)
f(x) = 0, otherwise
이거 왠지 될거같은데 이게 counter
이거 왠지 될거같은데 이게 counter example이라는 증명은 어떻게 해야할지 딱 감이 잘 안오네요;
+아아 이해갔습니다 굿!
원리적으로는 가능 할 것 같군요..
[0, 1]과 [0,1] X [0, 1]은 Cardinality가 같으니까요... 다만 함수를 어떻게 잡아야 하는 지는 잘 모르겠네요...
[0,1]과 [0,1]X[0,1]이
[0,1]과 [0,1]X[0,1]이 cardinality가 같다는 점은 이 문제와는 별 관계는 없을 것 같습니다.
왜냐하면 둘의 cardinality가 같다는 것은 g: [0,1] -> [0,1]X[0,1]인 bijection g가 있다는 것인데요..
이문제에서는 애초에 f:[0,1] -> [0,1]을 제시하라고 했기 때문에 g(x) = (x, f(x))를 만족해야 합니다.
그런데 이러한 bijection은 존재하지 않습니다. 간단한 예로만 봐도 g(x1)=(0,0)이라고 하면 g(x2)=(0,1)이 되는 x2는 있을 수 없죠.
따라서 제 생각에는 어떤 f:[0,1] -> [0,1]도 [0,1]x[0,1]의 모든 점을 커버할 수는 없기 때문에
애초에 문제에서 주어진 "면적이 있는" 직사각형이라는 점을 이용해야 될 것 같습니다.
유리수 집합 Q={p_1,p_2,...}이라
유리수 집합 Q={p_1,p_2,...}이라 하면
take q_1 from R-Q
Q_1={p_1+q_1, p_2+q_1, p_3+q_1,....}
take q_2 from R-(QUQ_1)
Q_2={p_1+q_2, p_2+q_2, p_3+q_2,....}
take q_3 from R-(QUQ_1UQ_2)
Q_3={p_1+q_3, p_2+q_3,.....}
:
:
0.we can construct Q_n for all n in N. (R uncountable)
1.Q_i, Q_j disjoint subsets of R for i!= j.
2.Q_i dense in R for all i.
f(x)=p_i if x in Q_i for some i, 0 otherwise.
then {(x,f(x))} dense in RxR.
심플하고 좋네요. 굿굿!!!
심플하고 좋네요. 굿굿!!! (치역을 [0,1]로 바운드만 시키면 끝)
무리수를 가지고 구축하셨는데.. 그럼 혹시 유리수만 사용해서 구축은 가능할까요? f(R-Q)=0 으로 해두고..
위의 Jick님의 함수 잘 들여다 보세요. 예로 큰
위의 Jick님의 함수 잘 들여다 보세요. 예로 큰 소수 p에 대해서, {(k/p,(mp+k)/p^2)| p prime, 0<= m, k<=p-1} 점들을 생각해보시면 됩니다. 제가 했던 방법 쓰시려면 Q_i={q/(p_i^n)|p_i is i-th prime, n in N, q in Z, gcd(p_i,q)=1 } 집합들을 생각하시구요. 저는 여기까지만.
설명감사합니다!
설명감사합니다!
이건 어떤가요.
f(n) =
{
n if n is rational
1/n if n is irrational.
}
...And all in war with Time for love of you,
As he takes from you, I engraft you new.
-Sonnet XV
전산계획설계사 지망 영문학과생
아, 아니군요.
실수...
...And all in war with Time for love of you,
As he takes from you, I engraft you new.
-Sonnet XV
전산계획설계사 지망 영문학과생
아무리 보아도 R->R로는 불가능합니다.
아무리 보아도 R->R로는 불가능합니다.
...And all in war with Time for love of you,
As he takes from you, I engraft you new.
-Sonnet XV
전산계획설계사 지망 영문학과생
assume possible. then there
assume possible.
then there exists f: R -> R such that
{ x, f(x) is dense in [0, 1] x [0, 1]
then for this f(x), consider x_0 != 1, and x_0 != 0 ( x_0 ∈ (0, 1) )
1. consider lim x1 -> x0+ f(x1) = f(x0). then there exists rectangle (x1, f(x1), x0, f(x0) ), (x0, f(x0)), (x1-x0, f(x1-x0)), (x0-x1, f(x0-x1)).
2. suppose lim x1-> x0+ f(x1) != f(x0)
then for every x1,
( lim x1->x0+ x1, lim x1->x0+ f(x1) ) != ( x0, f(x0) )
hence, a distinctive line (lim x1->x0, x1, lim x1->x0, f(x1)), (x0, f(x0) ) exists.
consider negative limit too.
case 2-1: trivial.
case 2-2: another line exists. with the coordinates of these two lines we can make rectangle.
QED
...And all in war with Time for love of you,
As he takes from you, I engraft you new.
-Sonnet XV
전산계획설계사 지망 영문학과생
그러니까...
그런 함수 f(x)가 있다고 가정합니다.
플러스 리미트(한쪽으로만 리미트를 거는 것)를 써서, 한 쪽으로 연속이 된다면 사각형은 만들 수 있습니다.(위에 많은 분들이 설명하였으니 이 부분은 trivial이라 생각하고 증명하지 않습니다.) 그러므로 경우 1인 경우엔 반증이 됩니다.
한 쪽으로 연속이 안 될 경우(경우 2라 지칭합니다), 그때 lim x1-> x0 x1, lim x1->x0 f(x1) 즉 좌표 (x0, f(x0))에 한 쪽에서 치닫는 좌표 어떤 것을 찾아도 x0, f(x0)와 다르므로 직선을 만들 수 있습니다.
즉, 4 가지의 경우가 있는데;
1-1: 경우 1이 있으면 무조건 반증됩니다.
1-2:
2-1:
그리고 2-2:
반대쪽도 똑같이 경우 2가 생길 경우, 좌표 ( x0, f(x0) )를 중심으로 직선 둘을 만들 수 있습니다. 좌표 (x1, f(x1)) 들은 전부 f(x)위에 놓여있으니 이 둘 사이에 f(x)는 가로지르지 않습니다.
f(x)에 닿지 않는 서로 다른 직선 둘을 만들었으니 이 둘을 이어 사각형을 만들 수 있습니다. 그러므로 경우 2-2도 반증이 됩니다.
...And all in war with Time for love of you,
As he takes from you, I engraft you new.
-Sonnet XV
전산계획설계사 지망 영문학과생
아...
이거도 아니군요.
선과 사각형을 만드는 건 좋은데 그 사이에 f(x)가 가로지르지 않는다는 보장이 없습니다.
그렇지 않는 경우를 상정할 수 있겠지만 이 상황에선 f(x)가 사각형 그리는 게 가능하지 않은 함수라고 상정한 거니까...
아음 R-> RxR은 dense하지 않지만... 아아악..
...And all in war with Time for love of you,
As he takes from you, I engraft you new.
-Sonnet XV
전산계획설계사 지망 영문학과생
문제에서 함수에 대한 아무런 제약이 없으니까 함수가
문제에서 함수에 대한 아무런 제약이 없으니까 함수가 리밋 값을 꼭 가진다고 보장할 수 없네요.
만약 리밋값이 존재한다면 모든 구간에서 불연속이라도 사각형을 구축 할 수 있습니다.
lim_{x1 -> +x0} f(x1) = b
리밋의 정의를 이용해 epsilon=0.1로 설정하고
|x - x0| < delta 이면 |b-f(x)| < epsilon인 delta를 fix 시킵니다.
그러면 다음 둘중에 한 사각형이 반드시 함수값을 포함하지 않습니다.
[x0 + delta/3, x0+delta/2] x [0, 0.2]
[x0 + delta/3, x0+delta/2] x [0.8, 1]
앗... 수학나라에 발을 잘못 디뎠군요... 역시
앗... 수학나라에 발을 잘못 디뎠군요...
역시 수학나라는 언어가 틀려.. ㅠ.ㅜ
전 일단 그래프 나오면 깨갱이라서리.. ㅎㅎㅎ;
jick님 솔루션 부연설명입니다. 살짝만 바꿔서,
jick님 솔루션 중학생도 이해 가능한 부연설명입니다. 살짝만 바꿔서, 함수f를 다음과 같이 정의를 하면. (mod는 정수 나누기 나머지입니다. 5 mod 2 = 1)
어떤 임의의 사각형에 대해서도 그 안에 한 점(x,f(x))을 찾을 수 있다는걸 증명합시다.
사각형이 [a,b]x[c,d]라고 합시다.(a,b가 가로, c,d가 세로, a < b, c < d)
먼저 다음 조건들을 만족하는 큰소수 p를 고릅니다.
1/p < b-a
1/p < d-c
1/p < a
그러면 c < n/p < d 를 만족하는 자연수 n이 존재하겠지요. 이제 f(x)= n/p와 a < x < b를 만족하는 x가 있으면 증명됩니다.
a < (n+pm)/(p^2) < b를 만족하는 자연수 m이 존재합니다, m이 1 차이날때마다 1/p만큼 차이가 나니까요.
x=(n+pm)/(p^2) 로 x를 설정.
f(x) = ((n+pm) mod p)/p = n/p 입니다. 끝.
나중에 시간 나면 zalamea님 솔루션도 쉬운 버젼으로 설명해볼게요.
없다. 증명 끝.
없다. 증명 끝.
세벌 https://sebuls.blogspot.kr/
지금 이 글타래 토론은 없고 서로 다른말만 하네요
지금 이 글타래 토론은 없고 서로 다른말만 하네요 ㅡㅡ)
특히나 제가 쓴 글에는 반박할 거리가 상당히 많음에도 조용하군요 ...
...
0 < X[0] < 1 에서 아무 숫자나 택하고
X[n+1] = 3.57 * X[n] * (1 - X[n]) 로 정의되는 매핑에 집어넣으면 (n >= 1)
0과 1사이를 중복도 없이 무한히 빼곡히 채우는 아름다운 수열이 나오니깐
어떤 사각형도 발붙이지 못하게 주어진 평면을 가득채우는 것 또한 간단(?)하지만,
...
but,,,
이 문제에 대해선 일종의 반칙으로(?) 간주될 것 같아서 그냥 패스합니다... >_<
음... 극한의 개념을 도입해보면 어떨까요?
극한의 개념을 도입해보는겁니다. 뭐 예를들어 y=무한대*x^무한대-무한대 의 경우 뭔가 가능하지 않을까요?
실수의 개념을 넣는거죠
그림을 보시면 아실 듯
그림을 보시면 될겁니다.
아 생각해보니깐
아 생각해보니깐 y=무한대*(x-0.000000000000000000000000000000000000000000000000000000000001)*(x-0.000000000000000000000000000000000000000000000000000000000000002)*...... 뭐 이런식으로 해야되는군요.
이렇게 한다면~_~... 적어도 직사각형에는 무조건
이렇게 한다면~_~... 적어도 직사각형에는 무조건 포함 될 수 있을거 같군요.
직사각형의 크기를 줄이고 줄여도 이 함수도 그 크기 만큼의 공간을 안남기려 할테니..
아놔 근데 저 위에 페뭐씨의 곡선이 있었군요
아놔 근데 저 위에 페뭐씨의 곡선이 있었군요 ㄱ-...제기랄..
전영역을 커버하면 함수가 아니지 않나요? 전영역을
전영역을 커버하면 함수가 아니지 않나요?
전영역을 커버 하려면 임의의 x의 1개 값에 대응해 여러개의 y 값이 나와야 하는데...
함수의 정의에 따르면 그런 것은 함수라고 부를 수는 없을거 같은데요.
Neogeo - Future is Now.